Câu 1:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \left( {x - 1} \right){e^{2x}},\) trục hoành và các đường thẳng \(x=0;x=2.\)
A. \(S = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} - \frac{3}{4}\)
B. \(S = \frac{{{e^4}}}{4} - \frac{{{e^2}}}{2} - \frac{3}{4}\)
C. \(S = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} + \frac{3}{4}\)
D. \(S = \frac{{{e^4}}}{4} - \frac{{{e^2}}}{2} + \frac{3}{4}\)
Câu 2:
Tính thể tích V của khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2x\) và \(y = - {x^2}\) quay quanh trục Ox.
A. \(V = \frac{4}{3}\)
B. \(V = \frac{4\pi}{3}\)
C. \(V = \frac{\pi}{3}\)
D. \(V = \frac{1}{3}\)
Câu 3:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y = x\sin 2x\), trục hoành và các đường thẳng \(x = 0,x = \pi .\)
A. \(S = 2\pi\)
B. \(S = \frac{\pi}{4}\)
C. \(S = \frac{\pi}{2}\)
D. \(S = \pi\)
Câu 4:
Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng N'\left( t \right) = \frac{{7000}}{{t + 2}} và lúc đầu đám vi trùng có 300 000 con. Sau 10 ngày, đám vi trùng có khoảng bao nhiêu con?
A. 317394 con
B. 312542 con
C. 307412 con
D. 322142 con
Câu 5:
Tính thể tích V của vật thể nằm giữa hai mặt phẳng \(x = 0;x = \pi\), biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\left( {0 \le x \le \pi } \right)\) là một tam giác đều có cạnh là \(2\sqrt {\sin x} .\)
A. \(V = \sqrt 3\)
B. \(V = \frac{\pi}{\sqrt 3}\)
C. \(V = 2\sqrt 3\)
D. \(V = 2\pi\)
Câu 6:
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x - {x^2}\) và Ox. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành.
A. \(V = \frac{{16\pi }}{{15}}\)
B. \(V = \frac{{136\pi }}{{15}}\)
C. \(V = \frac{{16}}{{15}}\)
D. \(V = \frac{{136 }}{{15}}\)
Câu 7:
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = {x^2}.{e^x}, trục hoành và đường thẳng x = 1.
A. S = e - 2
B. S = 2 + e
C. S = 2 - e
D. S = 1
Câu 8:
Một chiếc cổng Parabol cao 16m và 2 chân cổng cách nhau 8m như hình vẽ. Nhà thiết kế xây dựng xây 2 cây cột AD, BC cách nhau 4m (2 cây cột này đối xứng với nhau qua trục đối xứng của Parabol), 2 phần cổng nhỏ ở 2 bên dành cho xe máy và xe đạp qua lại và phần cổng to ở giữa chỉ dành riêng cho xe bus BRT. Tính diện tích phần thiết diện cổng dành cho xe bus BRT đi qua.

A. \(S = \frac{{176}}{3}\left( {{m^2}} \right)\)
B. \(S = \frac{{128}}{3}\left( {{m^2}} \right)\)
C. \(S = \frac{{64}}{3}\left( {{m^2}} \right)\)
D. \(S = \frac{{256}}{3}\left( {{m^2}} \right)\)
Câu 9:
Tính thể tích V của khối tròn xoay do hình phẳng giới hạn bởi đồ thị hàm số \(y=e^x\), trục hoành và hai đường thẳng x=0,x=3 quay quanh trục Ox tạo thành.
A. \(V = \frac{{\left( {{e^6} - 1} \right)\pi }}{2}\)
B. \(V = \frac{{{e^6} - 1}}{2}\)
C. \(V = \frac{{\left( {{e^6} + 1} \right)\pi }}{2}\)
D. \(V = \frac{{{e^6} + 1}}{2}\)
Câu 10:
Một ô tô đang chạy đều với vân tốc a(m/s) thì người lái xe đạp phanh. Từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số \(v(t) = - 5t + a\,(m/s),\) trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu a của ô tô là bao nhiêu, biết từ lúc đạp phanh đến khi dừng hản ô tô di chuyển được 40 mét.
A. a=20
B. a=10
C. a=40
D. a=25
Câu 11:
Viết công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2-1\), trục hoành và đường thẳng x = 2.
A. \(S = \int\limits_0^2 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
B. \(S = \int\limits_{ - 1}^1 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
C. \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 1} \right)d{\rm{x}}} } \right|\)
D. \(S = \int\limits_0^1 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
Câu 12:
Diện tích hình phẳng giới hạn bởi đường cong \(y = 2\sqrt {ax} \left( {a > 0} \right)\), trục hoành và đường thẳng x = a bằng \(ka^2\). Tính giá trị của tham số k.
A. \(k=\frac{7}{3}\)
B. \(k=\frac{4}{3}\)
C. \(k=\frac{12}{5}\)
D. \(k=\frac{6}{5}\)
Câu 13:
Cho hình phẳng (H) giới hạn bởi các đường \(y=x^2-2x\), trục hoành, trục tung, đường thẳng x = 1. Tính thể tích V hình tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox.
A. \(V = \frac{{8\pi }}{{15}}\)
B. \(V = \frac{{4\pi }}{3}\)
C. \(V = \frac{{15\pi }}{8}\)
D. \(V = \frac{{7\pi }}{8}\)
Câu 14:
Giả sử một vật đi từ trạng thái nghỉ t=0(s) chuyển động thẳng với vận tốc \(v\left( t \right) = t\left( {5 - t} \right)\left( {m/s} \right)\) . Tìm quãng đường vật đi được cho đến khi nó dừng lại.
A. \(s = \frac{{125}}{9}\left( m \right)\)
B. \(s = \frac{{125}}{12}\left( m \right)\)
C. \(s = \frac{{125}}{3}\left( m \right)\)
D. \(s = \frac{{125}}{6}\left( m \right)\)
Câu 15:
Cho parapol (P) \(y=x^2\) và hai điểm A, B thuộc (P) sao cho AB=2. Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB.

A. \(S_{max}=\frac{4}{3}\)
B. \(S_{max}=\frac{3}{4}\)
C. \(S_{max}=\frac{2}{3}\)
D. \(S_{max}=\frac{3}{2}\)
Câu 16:
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t) = 10t - {t^2},\) trong đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là bao nhiêu?
A. v = 5(m/p)
B. v = 9(m/p)
C. v = 3(m/p)
D. v = 7(m/p)
Câu 17:
Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = 0,\,y = x\sqrt {\ln (x + 1)}\) và x = 1 xung quanh trục Ox.
A. \(V = \frac{\pi }{{18}}(12\ln 2 - 5)\)
B. \(V = \frac{{5\pi }}{{18}}\)
C. \(V = \frac{{5\pi }}{{6}}\)
D. \(V = \frac{\pi }{6}(12\ln 2 - 5)\)
Câu 18:
Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = {x^3},y = 2 - x\) và y = 0. Mệnh đề nào sau đây là đúng?
A. \(S = \int\limits_0^1 {{x^3}dx} + \int\limits_1^2 {\left( {x - 2} \right)dx}\)
B. \(S = \frac{1}{2} + \int\limits_0^1 {{x^3}dx}\)
C. \(S = \left| {\int\limits_0^2 {({x^3} + x - 2)dx} } \right|\)
D. \(S=\int\limits_0^1 {\left| {{x^3} - (2 - x)} \right|dx}\)
Câu 19:
Một vật chuyển động chậm dần với vận tốc \(v\left( t \right) = 160 - 10t\left( {m/s} \right).\) Tìm quãng đường S mà vật di chuyển trong khoảng thời gian từ thời điểm đến thời điểm vật dừng lại.
A. S=2560(m)
B. S=1280(m)
C. S=2480(m)
D. S=3840(m)
Câu 20:
Cho hình phẳng (H ) giới hạn bởi các đường \(y = {x^2};y = 0;x = 2\). Tính thể tích V của khối tròn xoay thu được khi quay (H ) quanh trục Ox.
A. \(V = \frac{8}{3}\)
B. \(V = \frac{{32}}{5}\)
C. \(V = \frac{{8\pi }}{3}\)
D. \(V = \frac{{32\pi }}{5}\)
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \left( {x - 1} \right){e^{2x}},\) trục hoành và các đường thẳng \(x=0;x=2.\)
A. \(S = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} - \frac{3}{4}\)
B. \(S = \frac{{{e^4}}}{4} - \frac{{{e^2}}}{2} - \frac{3}{4}\)
C. \(S = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} + \frac{3}{4}\)
D. \(S = \frac{{{e^4}}}{4} - \frac{{{e^2}}}{2} + \frac{3}{4}\)
Ta có: \((x - 1){e^{2x}} = 0 \Leftrightarrow x = 1\)
Trên khoảng (0;2):
\(\begin{array}{l} (x - 1){e^{2x}} < 0 \Leftrightarrow 0 < x < 1\\ (x - 1){e^{2x}} > 0 \Leftrightarrow 1 < x < 2 \end{array}\)
Suy ra:
\(S = \int\limits_0^2 {\left| {\left( {x - 1} \right){e^{2x}}} \right|dx} = \int\limits_0^1 {\left( {1 - x} \right){e^{2x}}dx} + \int\limits_1^2 {\left( {x - 1} \right){e^{2x}}dx} = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} - \frac{3}{4}\)
Trên khoảng (0;2):
\(\begin{array}{l} (x - 1){e^{2x}} < 0 \Leftrightarrow 0 < x < 1\\ (x - 1){e^{2x}} > 0 \Leftrightarrow 1 < x < 2 \end{array}\)
Suy ra:
\(S = \int\limits_0^2 {\left| {\left( {x - 1} \right){e^{2x}}} \right|dx} = \int\limits_0^1 {\left( {1 - x} \right){e^{2x}}dx} + \int\limits_1^2 {\left( {x - 1} \right){e^{2x}}dx} = \frac{{{e^4}}}{4} + \frac{{{e^2}}}{2} - \frac{3}{4}\)
Tính thể tích V của khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2x\) và \(y = - {x^2}\) quay quanh trục Ox.
A. \(V = \frac{4}{3}\)
B. \(V = \frac{4\pi}{3}\)
C. \(V = \frac{\pi}{3}\)
D. \(V = \frac{1}{3}\)
Phương trình hoành độ giao điểm \({x^2} - 2x = - {x^2} \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\)
Do \(0> - {x^2} > {x^2} - 2x,\forall x \in \left[ {0;1} \right] \Rightarrow {\left( {{x^2} - 2x} \right)^2} > {\left( { - x} \right)^2},\forall x \in \left[ {0;1} \right]\) nên:
\(V = \pi \int\limits_0^1 {\left[ {{{\left( {{x^2} - 2x} \right)}^2} - {{\left( { - {x^2}} \right)}^2}} \right]dx} = \frac{\pi }{3}.\)
Do \(0> - {x^2} > {x^2} - 2x,\forall x \in \left[ {0;1} \right] \Rightarrow {\left( {{x^2} - 2x} \right)^2} > {\left( { - x} \right)^2},\forall x \in \left[ {0;1} \right]\) nên:
\(V = \pi \int\limits_0^1 {\left[ {{{\left( {{x^2} - 2x} \right)}^2} - {{\left( { - {x^2}} \right)}^2}} \right]dx} = \frac{\pi }{3}.\)
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y = x\sin 2x\), trục hoành và các đường thẳng \(x = 0,x = \pi .\)
A. \(S = 2\pi\)
B. \(S = \frac{\pi}{4}\)
C. \(S = \frac{\pi}{2}\)
D. \(S = \pi\)
Ta có \(S = \int\limits_0^\pi {\left| {x\sin 2x} \right|dx} = \int\limits_0^{\frac{\pi }{2}} {x\sin 2xdx} - \int\limits_{\frac{\pi }{2}}^\pi {x\sin 2xdx} = \pi\)
Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng N'\left( t \right) = \frac{{7000}}{{t + 2}} và lúc đầu đám vi trùng có 300 000 con. Sau 10 ngày, đám vi trùng có khoảng bao nhiêu con?
A. 317394 con
B. 312542 con
C. 307412 con
D. 322142 con
Ta có: \(N\left( t \right) = \int {\frac{{7000}}{{t + 2}}dt} = 7000.\ln \left| {t + 2} \right| + C\)
Với t=0 ta có: \(7000\ln 2 + C = 300000 \Rightarrow 295148\)
Với t=10 ta có: \(N(10) = 7000ln12 + 295148 = 312542\)
Với t=0 ta có: \(7000\ln 2 + C = 300000 \Rightarrow 295148\)
Với t=10 ta có: \(N(10) = 7000ln12 + 295148 = 312542\)
Tính thể tích V của vật thể nằm giữa hai mặt phẳng \(x = 0;x = \pi\), biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\left( {0 \le x \le \pi } \right)\) là một tam giác đều có cạnh là \(2\sqrt {\sin x} .\)
A. \(V = \sqrt 3\)
B. \(V = \frac{\pi}{\sqrt 3}\)
C. \(V = 2\sqrt 3\)
D. \(V = 2\pi\)
Gọi S(x) là diện tích của thiết diện đã cho thì: \(S\left( x \right) = {\left( {2\sqrt {\sin x} } \right)^2}.\frac{{\sqrt 3 }}{4} = \sqrt 3 \sin x.\)
Thể tích vật thể là: \(V = \int\limits_0^\pi {S\left( x \right)dx} = \int\limits_0^\pi {\sqrt 3 \sin xdx} = 2\sqrt 3 .\)
Thể tích vật thể là: \(V = \int\limits_0^\pi {S\left( x \right)dx} = \int\limits_0^\pi {\sqrt 3 \sin xdx} = 2\sqrt 3 .\)
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x - {x^2}\) và Ox. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành.
A. \(V = \frac{{16\pi }}{{15}}\)
B. \(V = \frac{{136\pi }}{{15}}\)
C. \(V = \frac{{16}}{{15}}\)
D. \(V = \frac{{136 }}{{15}}\)
Phương trình hoành độ giao điểm: \(2x - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\)
Khi đó thể tích khối tròn xoay là: \(V = \pi \int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} = \left. {\pi \left( {\frac{{4{x^3}}}{3} - {x^4} + \frac{{{x^5}}}{5}} \right)} \right|_0^2 = \frac{{16\pi }}{{15}}.\)
Khi đó thể tích khối tròn xoay là: \(V = \pi \int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} = \left. {\pi \left( {\frac{{4{x^3}}}{3} - {x^4} + \frac{{{x^5}}}{5}} \right)} \right|_0^2 = \frac{{16\pi }}{{15}}.\)
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = {x^2}.{e^x}, trục hoành và đường thẳng x = 1.
A. S = e - 2
B. S = 2 + e
C. S = 2 - e
D. S = 1
Phương trình hoành độ giao điểm \({x^2}{e^x} = 0 \Leftrightarrow x = 0\)
Ta có \(S = \int\limits_0^1 {\left| {{x^2}{e^x}} \right|dx} = \int\limits_0^1 {{x^2}{e^x}dx} = e - 2\)
Ta có \(S = \int\limits_0^1 {\left| {{x^2}{e^x}} \right|dx} = \int\limits_0^1 {{x^2}{e^x}dx} = e - 2\)
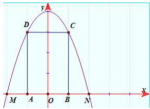
Một chiếc cổng Parabol cao 16m và 2 chân cổng cách nhau 8m như hình vẽ. Nhà thiết kế xây dựng xây 2 cây cột AD, BC cách nhau 4m (2 cây cột này đối xứng với nhau qua trục đối xứng của Parabol), 2 phần cổng nhỏ ở 2 bên dành cho xe máy và xe đạp qua lại và phần cổng to ở giữa chỉ dành riêng cho xe bus BRT. Tính diện tích phần thiết diện cổng dành cho xe bus BRT đi qua.
A. \(S = \frac{{176}}{3}\left( {{m^2}} \right)\)
B. \(S = \frac{{128}}{3}\left( {{m^2}} \right)\)
C. \(S = \frac{{64}}{3}\left( {{m^2}} \right)\)
D. \(S = \frac{{256}}{3}\left( {{m^2}} \right)\)
Chọn hệ trục như hình vẽ \(M\left( { - 4;0} \right);N\left( {4;0} \right)\)
Khi đó phương trình Parabol có dạng
\(y = a{x^2} + bx + c = a\left( {x - 4} \right)\left( {x + 4} \right)\) (vì parabol cắt trục Ox tại M và N).
Mặt khác Parabol đi qua điểm \(\left( {0;16} \right) \Rightarrow a = - 1\)
Do đó \(\left( P \right):y = 16 - {x^2}\)
Khi đó diện tích cổng to là \(S = \int\limits_{ - 2}^2 {\left( {16 - {x^2}} \right)dx} = \left. {\left( {16x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^2 = \frac{{176}}{3}\left( {{m^2}} \right)\)
Khi đó phương trình Parabol có dạng
\(y = a{x^2} + bx + c = a\left( {x - 4} \right)\left( {x + 4} \right)\) (vì parabol cắt trục Ox tại M và N).
Mặt khác Parabol đi qua điểm \(\left( {0;16} \right) \Rightarrow a = - 1\)
Do đó \(\left( P \right):y = 16 - {x^2}\)
Khi đó diện tích cổng to là \(S = \int\limits_{ - 2}^2 {\left( {16 - {x^2}} \right)dx} = \left. {\left( {16x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^2 = \frac{{176}}{3}\left( {{m^2}} \right)\)
Tính thể tích V của khối tròn xoay do hình phẳng giới hạn bởi đồ thị hàm số \(y=e^x\), trục hoành và hai đường thẳng x=0,x=3 quay quanh trục Ox tạo thành.
A. \(V = \frac{{\left( {{e^6} - 1} \right)\pi }}{2}\)
B. \(V = \frac{{{e^6} - 1}}{2}\)
C. \(V = \frac{{\left( {{e^6} + 1} \right)\pi }}{2}\)
D. \(V = \frac{{{e^6} + 1}}{2}\)
\(V = \pi \int\limits_0^3 {{{\left( {{e^x}} \right)}^2}dx = \pi \int\limits_0^3 {{e^{2x}}dx = \frac{\pi }{2}{e^{2x}}\left| {\begin{array}{*{20}{c}} 3\\ 0 \end{array}} \right. = \frac{\pi }{2}\left( {{e^6} - 1} \right)} }\)
Một ô tô đang chạy đều với vân tốc a(m/s) thì người lái xe đạp phanh. Từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số \(v(t) = - 5t + a\,(m/s),\) trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu a của ô tô là bao nhiêu, biết từ lúc đạp phanh đến khi dừng hản ô tô di chuyển được 40 mét.
A. a=20
B. a=10
C. a=40
D. a=25
Khi xe dừng hẳn vận tốc bằng 0 nên: \(- 5t + a = 0 \Leftrightarrow t = \frac{a}{5}.\)
Ta có: \(S = \int\limits_0^{\frac{a}{5}} {v(t)dt} = \int\limits_0^{\frac{a}{5}} {( - 5t + a)dt} = \frac{1}{{10}}{a^2}\)
\(S = 40 \Leftrightarrow \frac{1}{{10}}{a^2} = 40 \Rightarrow a = 20.\)
Ta có: \(S = \int\limits_0^{\frac{a}{5}} {v(t)dt} = \int\limits_0^{\frac{a}{5}} {( - 5t + a)dt} = \frac{1}{{10}}{a^2}\)
\(S = 40 \Leftrightarrow \frac{1}{{10}}{a^2} = 40 \Rightarrow a = 20.\)
Viết công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=x^2-1\), trục hoành và đường thẳng x = 2.
A. \(S = \int\limits_0^2 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
B. \(S = \int\limits_{ - 1}^1 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
C. \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 1} \right)d{\rm{x}}} } \right|\)
D. \(S = \int\limits_0^1 {\left| {{x^2} - 1} \right|d{\rm{x}}}\)
Phương trình hoành độ giao điểm của đồ thị hàm số \(y=x^2-1\) và trục hoành: \({x^2} - 1 = 0 \Leftrightarrow x = \pm 1\)
\(\Rightarrow S = \int\limits_{ - 1}^1 {\left| {{x^2} - 1} \right|dx} + \int\limits_1^2 {\left| {{x^2} - 1} \right|dx} = \int\limits_{ - 1}^2 {\left| {{x^2} - 1} \right|dx}\)
\(\Rightarrow S = \int\limits_{ - 1}^1 {\left| {{x^2} - 1} \right|dx} + \int\limits_1^2 {\left| {{x^2} - 1} \right|dx} = \int\limits_{ - 1}^2 {\left| {{x^2} - 1} \right|dx}\)
Diện tích hình phẳng giới hạn bởi đường cong \(y = 2\sqrt {ax} \left( {a > 0} \right)\), trục hoành và đường thẳng x = a bằng \(ka^2\). Tính giá trị của tham số k.
A. \(k=\frac{7}{3}\)
B. \(k=\frac{4}{3}\)
C. \(k=\frac{12}{5}\)
D. \(k=\frac{6}{5}\)
\(S = \int\limits_0^a {\left| {2\sqrt {ax} } \right|dx} = 2\sqrt a .\left. {\frac{2}{3}.{x^{\frac{3}{2}}}} \right|_0^a = \frac{4}{3}{a^2} = k{a^2} \Rightarrow k = \frac{4}{3}\)
Cho hình phẳng (H) giới hạn bởi các đường \(y=x^2-2x\), trục hoành, trục tung, đường thẳng x = 1. Tính thể tích V hình tròn xoay sinh ra bởi (H) khi quay (H) quanh trục Ox.
A. \(V = \frac{{8\pi }}{{15}}\)
B. \(V = \frac{{4\pi }}{3}\)
C. \(V = \frac{{15\pi }}{8}\)
D. \(V = \frac{{7\pi }}{8}\)
\(V = \pi \int\limits_0^1 {{{\left( {{x^2} - 2x} \right)}^2}dx} = \pi \int\limits_0^1 {\left( {{x^4} - 4{x^3} + 4{x^2}} \right)dx}\)
\(= \left. {\pi \left( {\frac{{{x^5}}}{5} - {x^4} + 4\frac{{{x^3}}}{3}} \right)} \right|_0^1 = \frac{{8\pi }}{{15}}.\)
\(= \left. {\pi \left( {\frac{{{x^5}}}{5} - {x^4} + 4\frac{{{x^3}}}{3}} \right)} \right|_0^1 = \frac{{8\pi }}{{15}}.\)
Giả sử một vật đi từ trạng thái nghỉ t=0(s) chuyển động thẳng với vận tốc \(v\left( t \right) = t\left( {5 - t} \right)\left( {m/s} \right)\) . Tìm quãng đường vật đi được cho đến khi nó dừng lại.
A. \(s = \frac{{125}}{9}\left( m \right)\)
B. \(s = \frac{{125}}{12}\left( m \right)\)
C. \(s = \frac{{125}}{3}\left( m \right)\)
D. \(s = \frac{{125}}{6}\left( m \right)\)
Khi vật dừng lại, vận tốc của vật bằng 0.
Ta có \(t\left( {5 - t} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} t = 0\\ t = 5 \end{array} \right.\)
Quãng đường vật đi được cho đến khi nó dừng lại: \(s = \int\limits_0^5 {t\left( {5 - t} \right)dt} = \left. {\left( {\frac{{5{t^2}}}{2} - \frac{{{t^3}}}{3}} \right)} \right|_0^5 = \frac{{125}}{6}\)
Ta có \(t\left( {5 - t} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} t = 0\\ t = 5 \end{array} \right.\)
Quãng đường vật đi được cho đến khi nó dừng lại: \(s = \int\limits_0^5 {t\left( {5 - t} \right)dt} = \left. {\left( {\frac{{5{t^2}}}{2} - \frac{{{t^3}}}{3}} \right)} \right|_0^5 = \frac{{125}}{6}\)
Cho parapol (P) \(y=x^2\) và hai điểm A, B thuộc (P) sao cho AB=2. Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi (P) và đường thẳng AB.
A. \(S_{max}=\frac{4}{3}\)
B. \(S_{max}=\frac{3}{4}\)
C. \(S_{max}=\frac{2}{3}\)
D. \(S_{max}=\frac{3}{2}\)
Giả sử \(A(a,{a^2}),\,B(b,{b^2}) \in \left( P \right)\,(b > a)\) sao cho: AB = 2
Phương trình đường thẳng AB có dạng: \(y = \frac{{\left( {{b^2} - {a^2}} \right)}}{{(b - a)}}x + m \Leftrightarrow y = (b + a)x + m\)
Thay tọa độ \(A(a;a^2)\) ta có: \({a^2} = (b + a)a + m \Rightarrow m = - ba\)
Vậy phương trình đường thẳng AB là: \(y=(b+a)x-ab\)
Gọi S là diện tích hình phẳng cần tìm ta có:
\(S = \int\limits_a^b {\left| {(b + a)x - ab - {x^2}} \right|dx} = \int\limits_a^b {\left[ {(b + a)x - ab - {x^2}} \right]dx} = \frac{1}{6}{(b - a)^3}\)\(\begin{array}{l} AB = 2 \Rightarrow {\left( {b - a} \right)^2} + {({b^2} - {a^2})^2} = 4 \Leftrightarrow {(b - a)^2}(1 + {(a + b)^2}) = 4\\ \Rightarrow \left| {b - a} \right| = b - a \le 2\,(do\,1 + {(a + b)^2} \ge 1,\forall a,b) \end{array}\)Vậy: \(S_{max}=\frac{4}{3}\)
Phương trình đường thẳng AB có dạng: \(y = \frac{{\left( {{b^2} - {a^2}} \right)}}{{(b - a)}}x + m \Leftrightarrow y = (b + a)x + m\)
Thay tọa độ \(A(a;a^2)\) ta có: \({a^2} = (b + a)a + m \Rightarrow m = - ba\)
Vậy phương trình đường thẳng AB là: \(y=(b+a)x-ab\)
Gọi S là diện tích hình phẳng cần tìm ta có:
\(S = \int\limits_a^b {\left| {(b + a)x - ab - {x^2}} \right|dx} = \int\limits_a^b {\left[ {(b + a)x - ab - {x^2}} \right]dx} = \frac{1}{6}{(b - a)^3}\)\(\begin{array}{l} AB = 2 \Rightarrow {\left( {b - a} \right)^2} + {({b^2} - {a^2})^2} = 4 \Leftrightarrow {(b - a)^2}(1 + {(a + b)^2}) = 4\\ \Rightarrow \left| {b - a} \right| = b - a \le 2\,(do\,1 + {(a + b)^2} \ge 1,\forall a,b) \end{array}\)Vậy: \(S_{max}=\frac{4}{3}\)
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t) = 10t - {t^2},\) trong đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là bao nhiêu?
A. v = 5(m/p)
B. v = 9(m/p)
C. v = 3(m/p)
D. v = 7(m/p)
\(v(t) = 10t - {t^2}\)
\(s(t) = \int {(10t - {t^2})dt} = 5{t^2} - \frac{{{t^3}}}{3} + C\)
Khi t=0 thì S=0 suy ra C=0
Tại \(t = {t_0} \Rightarrow s = 162:[/B] - \frac{{{t^3}}}{3} + 5{t^2} - 162 = 0 \Leftrightarrow \left[ \begin{array}{l} t = 9\\ t = - 4,937\\ t = 10,9 \end{array} \right.\)
Loại t=-4,937 vì thời gian không âm.
Loại t=10,9 vì khi thay vào vận tốc âm.
Vậy t=9 là giá trị cần cần tìm suy ra: \(v(9)=10.9-9^2=9\)
\(s(t) = \int {(10t - {t^2})dt} = 5{t^2} - \frac{{{t^3}}}{3} + C\)
Khi t=0 thì S=0 suy ra C=0
Tại \(t = {t_0} \Rightarrow s = 162:[/B] - \frac{{{t^3}}}{3} + 5{t^2} - 162 = 0 \Leftrightarrow \left[ \begin{array}{l} t = 9\\ t = - 4,937\\ t = 10,9 \end{array} \right.\)
Loại t=-4,937 vì thời gian không âm.
Loại t=10,9 vì khi thay vào vận tốc âm.
Vậy t=9 là giá trị cần cần tìm suy ra: \(v(9)=10.9-9^2=9\)
Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = 0,\,y = x\sqrt {\ln (x + 1)}\) và x = 1 xung quanh trục Ox.
A. \(V = \frac{\pi }{{18}}(12\ln 2 - 5)\)
B. \(V = \frac{{5\pi }}{{18}}\)
C. \(V = \frac{{5\pi }}{{6}}\)
D. \(V = \frac{\pi }{6}(12\ln 2 - 5)\)
\(V = \pi \int\limits_0^1 {{x^2}\ln (x + 1)dx}\)
Đặt: \(\left\{ \begin{array}{l} u = \ln (x + 1)\\ dv = {x^2}dx \end{array} \right. \Rightarrow \left\{ \begin{array}{l} du = \frac{1}{{x + 1}}dx\\ v = \frac{1}{3}{x^3} \end{array} \right.\)
Vậy:
\(\begin{array}{l} V = \pi \left[ {\left. {\frac{{{x^3}}}{3}\ln (x + 1)} \right|_0^1 - \frac{1}{3}\int\limits_0^1 {\frac{{{x^3}}}{{x + 1}}dx} } \right] = \pi \left[ {\frac{1}{3}\ln 2 - \int\limits_0^1 {\left( {\frac{{{x^3} + 1}}{{x + 1}} - \frac{1}{{x + 1}}} \right)dx} } \right]\\ = \pi \left[ {\frac{1}{3}\ln 2 - \int\limits_0^1 {\left( {({x^2} - x + 1) - \frac{1}{{x + 1}}} \right)dx} } \right] = \frac{\pi }{{18}}(12\ln 2 - 5). \end{array}\)
Đặt: \(\left\{ \begin{array}{l} u = \ln (x + 1)\\ dv = {x^2}dx \end{array} \right. \Rightarrow \left\{ \begin{array}{l} du = \frac{1}{{x + 1}}dx\\ v = \frac{1}{3}{x^3} \end{array} \right.\)
Vậy:
\(\begin{array}{l} V = \pi \left[ {\left. {\frac{{{x^3}}}{3}\ln (x + 1)} \right|_0^1 - \frac{1}{3}\int\limits_0^1 {\frac{{{x^3}}}{{x + 1}}dx} } \right] = \pi \left[ {\frac{1}{3}\ln 2 - \int\limits_0^1 {\left( {\frac{{{x^3} + 1}}{{x + 1}} - \frac{1}{{x + 1}}} \right)dx} } \right]\\ = \pi \left[ {\frac{1}{3}\ln 2 - \int\limits_0^1 {\left( {({x^2} - x + 1) - \frac{1}{{x + 1}}} \right)dx} } \right] = \frac{\pi }{{18}}(12\ln 2 - 5). \end{array}\)
Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = {x^3},y = 2 - x\) và y = 0. Mệnh đề nào sau đây là đúng?
A. \(S = \int\limits_0^1 {{x^3}dx} + \int\limits_1^2 {\left( {x - 2} \right)dx}\)
B. \(S = \frac{1}{2} + \int\limits_0^1 {{x^3}dx}\)
C. \(S = \left| {\int\limits_0^2 {({x^3} + x - 2)dx} } \right|\)
D. \(S=\int\limits_0^1 {\left| {{x^3} - (2 - x)} \right|dx}\)
Phương trình hoành độ giao điểm của đường thẳng y = 2 - x và đường cong y = x3 là:
\({x^3} = 2 - x \Leftrightarrow {x^3} + x - 2 = 0 \Leftrightarrow x = 1\)

Vậy diện tích hình phẳng là: \(S = {S_{OAB}} + {S_{ABC}} = \int\limits_0^1 {{x^3}dx} + \frac{1}{2}.\)
\({x^3} = 2 - x \Leftrightarrow {x^3} + x - 2 = 0 \Leftrightarrow x = 1\)
Vậy diện tích hình phẳng là: \(S = {S_{OAB}} + {S_{ABC}} = \int\limits_0^1 {{x^3}dx} + \frac{1}{2}.\)
Một vật chuyển động chậm dần với vận tốc \(v\left( t \right) = 160 - 10t\left( {m/s} \right).\) Tìm quãng đường S mà vật di chuyển trong khoảng thời gian từ thời điểm đến thời điểm vật dừng lại.
A. S=2560(m)
B. S=1280(m)
C. S=2480(m)
D. S=3840(m)
Khi vật dừng lại thì \(v\left( t \right) = 160 - 10t\left( {m/s} \right) = 0 \Leftrightarrow t = 16\)
Quãng đường vật đi được là \(S = \int_0^{16} {\left( {160 - 10t} \right)dt = \left. {\left( {160t - 5{t^2}} \right)} \right|} _0^{16} = 1280.\)
Quãng đường vật đi được là \(S = \int_0^{16} {\left( {160 - 10t} \right)dt = \left. {\left( {160t - 5{t^2}} \right)} \right|} _0^{16} = 1280.\)
Cho hình phẳng (H ) giới hạn bởi các đường \(y = {x^2};y = 0;x = 2\). Tính thể tích V của khối tròn xoay thu được khi quay (H ) quanh trục Ox.
A. \(V = \frac{8}{3}\)
B. \(V = \frac{{32}}{5}\)
C. \(V = \frac{{8\pi }}{3}\)
D. \(V = \frac{{32\pi }}{5}\)
Thể tích cần tính là \(V = \pi \int\limits_0^2 {{x^4}dx = \pi .\left. {\frac{{{x^5}}}{5}} \right|} _0^2 = \frac{{32\pi }}{5}\)